Bayesian Multilevel Modelling using PyStan

This is a tutorial, following through Chris Fonnesbeck's primer on using PyStan with Bayesian Multilevel Modelling.

1. Introduction

• Multilevel model: a regression model in which constituent model parameters are given probability models, which implies that they can vary by group. These are generalisations of regression modelling.
• Hierarchical model: a multilevel model where parameters are nested within one another.

Example: Radon contamination

Radon is a radioactive gas that enters homes through contact points with the ground, and is responsible for causing lung cancer. The distribution of radon varies with geographical location, dependent on the prevailing geology (influence of UK geology on radon concentration)

• More information about radon.

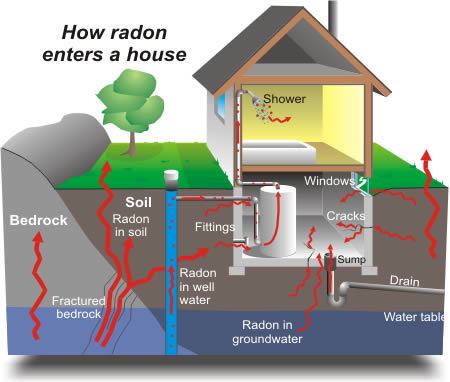
The EPA conducted a study of radon levels in 80,000 houses. There were two important predictors if the measured radon level:

• whether measurement was in the basement, or on the ground floor (radon levels are expected to be higher in basements)
• local uranium level (expected to correlate positively with radon level)

We will model radon levels in a single US state: Minnesota.

In this example, measurements are made at household level, and households exist within counties, which exist within the state. Hence the hierarchical model is that households are contained within counties, which are contained within the state.

Comments

In the first instance, we have a model where output is measured radon level as a function of the floor of the house at which the radon was measured (basement or ground floor), and the prevailing radon level.

Our estimate of the parameter of prevailing radon level for the region can be considered a prediction (as it is not measured directly).

The prevailing radon level may be taken to be that for the state (counties pooled) or that for the county (unpooled), or as some intermediate representation.

The model is multilevel/hierarchical because we are estimating parameters for individual households that exist within counties (which exist within the state), where the parameters vary at the level of the household within a state (i.e. between households), but also vary conditioned on the counties in which the households are found.

We already have the model outputs: data for household radon level measurements, associated with their counties; and inputs: the floor level at which the measurements were taken. We are attempting to estimate the parameters for alternative formulations of the model, and to assess which model is the best explanation for the observed data/best predictor for prevailing radon level. With a good model, we could go forward to predict new radon levels, given the information of the county, and the floor at which measurement was taken.